AI分类问题预测的是离散类别(如信用优/差、垃圾邮件/正常邮件),其评估指标围绕混淆矩阵展开的。测试集用于评估模型的性能。在模型训练完成后,我们会使用测试集来评估某一模型在未见过的数据上的表现,以了解模型的泛化能力。通过测试集的评估,我们会得到一些最终的评估指标。
一、混淆矩阵
混淆矩阵(Confusion Matrix)是分类模型性能评估的基础工具,而评估指标(如准确率、精确率、召回率等)则是从混淆矩阵中提取的量化结果。
“混淆”(Confusion)表示模型在分类任务中因”混淆”(即搞混、分错)不同类别而产生的错误。例如:将实际为A类的样本误判为B类,或将B类误判为A类。这个词直接反映了分类结果的混乱程度。”矩阵”(Matrix)指以矩阵形式(表格)结构化地展示分类结果,通常是一个N×N的方阵(N为类别数)。行代表真实类别,列代表预测类别,矩阵中的数值表示样本数量。
使用示例来解释:假如我们给信贷机构做了一个模型,这个模型可以预测人信用的优和差。我们把(实际)信用好的人定义为Positive(即正类);(实际)信用差的人,定义为Negative(即负类)。再用True(T)代表模型预测结果正确,False(F)代表模型预测错误。
| 预测为正类(信用优) | 预测为负类(信用差) | |
|---|---|---|
| 实际为正类(信用优) | True Positive – TP(真正例):实际为正类,模型正确预测为正类。 | False Negative – FN(假反例):实际为正类,模型错误预测为负类(漏报)。 |
| 实际为负类(信用差) | False Positive – FP(假正例):实际为负类,模型错误预测为正类(误报)。 | True Negative – TN(真反例):实际为负类,模型正确预测为负类。 |
说明:第二个字母P或N代表:对于一组样本,模型预测为正类或负类。第一个字母T或F代表:对于该组样本,模型预测结果是正确或错误。
我们一共准备了100个样本数据,其中60个是信用优,40个信用差。针对这100个样本数据,模型预测出了65个信用优,但其中48个人预测对了,17个预测错了。
解析题目:
- 实际信用优(正类):60人
- 实际信用差(负类):40人
- 模型预测信用优:65人(其中48人预测正确,17人预测错误)
关键项计算:
- 真正例 (TP):实际信用优且预测为信用优 = 48人
- 假正例 (FP):实际信用差但预测为信用优 = 17人(因为模型总预测信用优65人,其中48人预测正确,剩下17人预测错误)
- 假反例 (FN):实际信用优但预测为信用差 = 实际信用优总数 – 真正例TP = 60 – 48 = 12人
- 真反例 (TN):实际信用差且预测为信用差 = 实际信用差总数 – FP = 40 – 17 = 23人
得出混淆矩阵如下:
| 预测信用优 | 预测信用差 | 总计 | |
|---|---|---|---|
| 实际信用优 (正类) | TP = 48 | FN = 12 | 实际为正类60 |
| 实际信用差 (负类) | FP = 17 | TN = 23 | 实际为负类40 |
| 总计 | 模型预测为正例的总数65 | 模型预测为反例总数35 | 100 |
验证逻辑:
- 模型预测信用优总数 = TP + FP = 48 + 17 = 65(符合题目)
- 实际信用优总数 = TP + FN = 48 + 12 = 60(符合)
- 实际信用差总数 = FP + TN = 17 + 23 = 40(符合)
二、评估指标
在机器学习和数据科学中,准确率、精确率、召回率和F1分数是常用的评估指标,用于衡量分类模型的性能。我们一般会使用测试集来评估某一模型在未见过的数据上的表现,以了解模型的泛化能力。以下是评估指标的定义、计算方法以及各自的优缺点:
1、准确率(Accuracy)
准确率是指评估模型正确预测的样本数占总样本数的比例。
准确率 = (预测正确的样本数) / (总样本数) = (TP+TN)/(TP+TN+FP+FN)
根据信用评估矩阵图,我们可以得到:准确率 = (TP + TN) / 总数 = (48 + 23) / 100 = 71%
适用场景:当类别之间样本数量相对平衡(比如1:1),准确率可以整体判断模型预测的正确程度。可初步评估模型整体表现,快速判断模型是否优于随机猜测。
当类别之间样本数量不平衡时,准确率可能不是一个好的指标。
- 例如,在100个苹果中,有1个是坏苹果,99个是好苹果。设计好苹果为正类。这时候如果我们全部判断为好苹果,准确率可达到99%,但实际生活中往往我们需要找出那个坏的苹果,此时使用该指标就会存在偏差,因此我们需要根据实际业务场景选择合适的指标进行评估。
- 例如,假设某亚热带城市每百年只有 25 天会下雪(正类)。由于无雪天数(负类)远远多于有雪天数(正类),因此该城市的下雪数据集存在类别不平衡。设想一个二元分类模型,该模型原本应该预测每天会下雪或不会下雪,但实际上每天都预测“不会下雪”。该模型准确率很高,但预测能力不强。
在评估在类别不平衡数据集上训练的模型时, 精确度和召回率通常比准确度更有用。
2、精确率(Precision)
精确率是指评估模型预测为正类的样本中,实际为正类的比例。
精确率 = TP / (TP+FP)
根据信用评估矩阵图,我们可以得到:精确率 = TP / (TP + FP) = 48 / 65 ≈ 73.8% 说明:模型预测为信用优的样本中(总数为65个人),仅73.8%是真实的信用优。
适用场景:
- 精确率高意味着模型预测为正类的样本中,真正为正类的比例高,适用于只关注预测为正类的准确性的场景。在资源有限场景下:如营销活动仅针对预测为信用优的客户,需确保目标群体精准。
- 为了减少误判成本时候:当将信用差误判为信用优(FP)的代价较高时。例子:银行贷款审批中,误将高风险客户放贷(FP)可能导致坏账损失,需高精确率。
3、召回率(Recall)/真实阳性率
召回率是指实际为正类的样本中,被正确预测的比例,即真实阳性率(TPR)。
召回率 = TP / (TP+FN)
根据信用评估矩阵图,我们可以得到:实际信用为优的总数为60,其中48人预测正确,召回率 = TP / (TP + FN) = 48 / 60 = 80% 说明:模型能识别出80%的真实信用优用户。
适用场景:
- 召回率高意味着模型能够识别出更多的正类,适用于关注模型覆盖正类的能力的场景。例如,当我们想衡量100个苹果中,是否把市场中坏苹果(阳性)全部召回时,可以使用该指标。在一些“宁可错杀一千,绝不放过一个”的场景中,更加看中召回率。
- 当漏判正类/信用优(FN)的代价更高时,期望避免遗漏关键样本:
- 信用评分中若优质客户被拒绝(FN)可能损失收入的时候。
- 在医疗诊断中,漏诊患者(FN)比误诊健康人(FP)更严重的时候;
局限性:在不平衡的数据集中,实际阳性数量非常非常低,总共只有 1-2 个例子,召回率作为一种指标来说意义不大,用处也不大。
4、F1分数(F1 Score)
F1分数是精确率和召回率的调和平均数,用于综合考虑分类模型的准确性和召回能力。
F1分数 = 2 * (精确率 * 召回率) / (精确率 + 召回率)。
根据信用评估矩阵图,我们可以得到:F1分数 = 2 × (Precision × Recall) / (Precision + Recall) ≈ 76.8%
适用场景:F1分数同时考虑了精确率和召回率,适用于希望模型在精确率和召回率上都表现良好的场景。
5、ROC曲线和AUC
真阳性率和假阳性率
对于每个混淆矩阵,我们计算两个指标:真阳性率/召回率 (TPR – True Positive Rate) 与假阳性率 (FPR – False Positive Rate) 。
真阳性率 TPR = TP / (TP+FN)
TPR的意义:在所有实际为正类的样本中,模型正确预测为正类的比例。
- 高TPR:模型能有效识别正类(如疾病患者、欺诈交易)。
- 低TPR:模型漏检严重(FN多)。
假阳性率 FPR = FP / (FP+TN)
FPR的意义:在所有实际为负类的样本中,模型错误预测为正类的比例。
- 高FPR:模型误判多(如将健康人误诊为患者)。
- 低FPR:模型对负类的判断严格(FP少)。
TPR(真阳性率)和 FPR(假阳性率)是分类模型性能的两个关键指标,它们的数值关系反映了模型在识别正类和避免误判负类之间的权衡。两者通过分类阈值间接关联,但不存在直接的数学公式关系。
- TPR:衡量模型捕捉正类的能力,越高越好。
- FPR:衡量模型误判负类的风险,越低越好。
直观解释:
| 情况 | TPR(真阳性率) | FPR(假阳性率) |
|---|---|---|
| 理想模型 | 接近1(所有正类均被检出) | 接近0(无负类被误判) |
| 随机猜测 | 等于FPR(无区分能力) | 等于TPR(对角线) |
| 实际模型 | 越高越好,但需平衡FPR | 越低越好,但可能牺牲TPR |
示例(医疗检测):
- TPR=0.9:90%的患者被正确诊断,但可能有10%漏诊(FN)。
- FPR=0.1:10%的健康人被误诊为患者(FP)。
ROC曲线
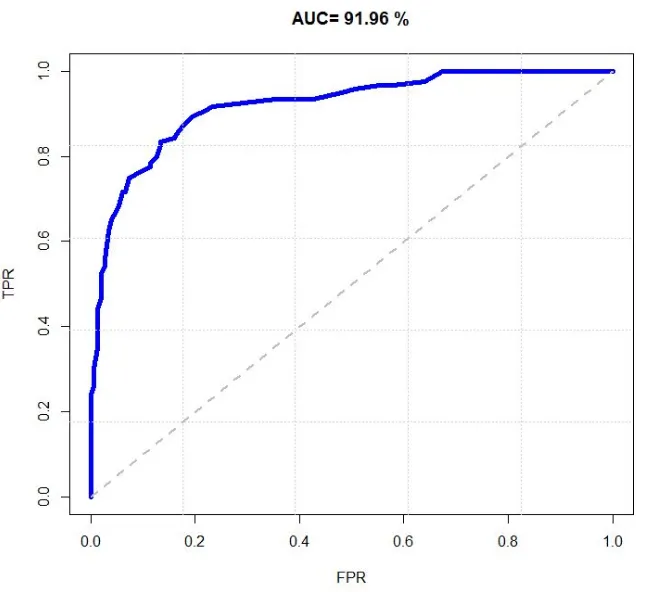
以FPR为x轴,TPR为y轴画图,就得到了ROC曲线。ROC的全称是“受试者工作特征”(Receiver Operating Characteristic)。受试者为分类模型。ROC曲线最初用于二战中雷达信号检测,区分真实目标如敌机和噪声如云层。后推广至医学诊断、机器学习等领域。
ROC曲线通过对TPR和FPR的权衡,帮助人们选择最佳分类阈值。一般来说,如果ROC是光滑的,那么基本可以判断没有太大的过拟合/OverFitting。ROC 曲线越靠近左上角,表示模型的性能越好。
AUC-ROC曲线下面积
AUC – Area Under the Curve(曲线下面积)为ROC曲线与横轴围成的面积。AUC直译为“ROC曲线下面积”,用于量化模型整体分类性能。AUC面积越高,表示模型区分正负样本的能力越强。AUC 的取值范围是 0 到 1,0.5 表示模型为随机分类器,1 表示模型为完美分类器。
三、总结
通过理解这些指标的定义、计算方法以及各自的优缺点,可以更好地评估和优化机器学习模型的性能。在实际应用中,应根据具体任务选择合适的评估指标。