反向传播是深度学习商用的基石性突破 – 甲壳虫AI(竞赛)案例精选

合集：AI基础-深度学习/神经网络

AI问题：AI计算模型

官网：https://www.AiSelect.club

本案例数据集和源码托管网址：MNIST1994手写数字图片数据集和CNN模型 – 甲壳虫AI(竞赛)案例精选

一、神经网络

神经网络是一种受人类大脑神经结构启发的计算模型，广泛应用于模式识别、分类、回归等任务中。它通过多层神经元的层级结构对数据进行逐层处理，从而从复杂的非线性数据中提取特征和模式。

1、神经元的工作方式

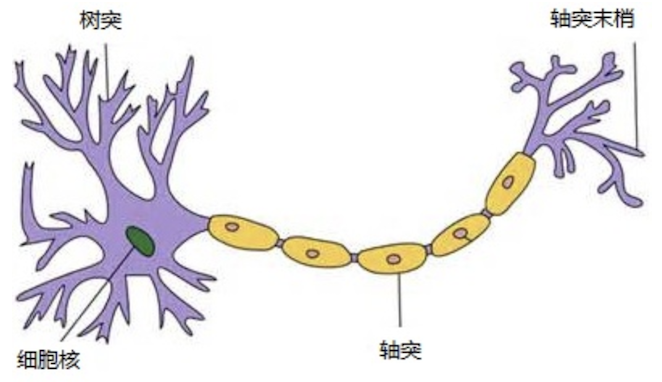
图：生物神经元

人工神经元接收到一个或多个输入，对他们进行加权并相加，总和通过一个非线性函数（激活函数）产生输出。

所有的输入xi，与相应的权重 wi 相乘并求和，然后加上参数 b，最后将求和结果送入到激活函数f()中，得到最终的输出结果。人工神经元特点是：多个输入、一个输出。

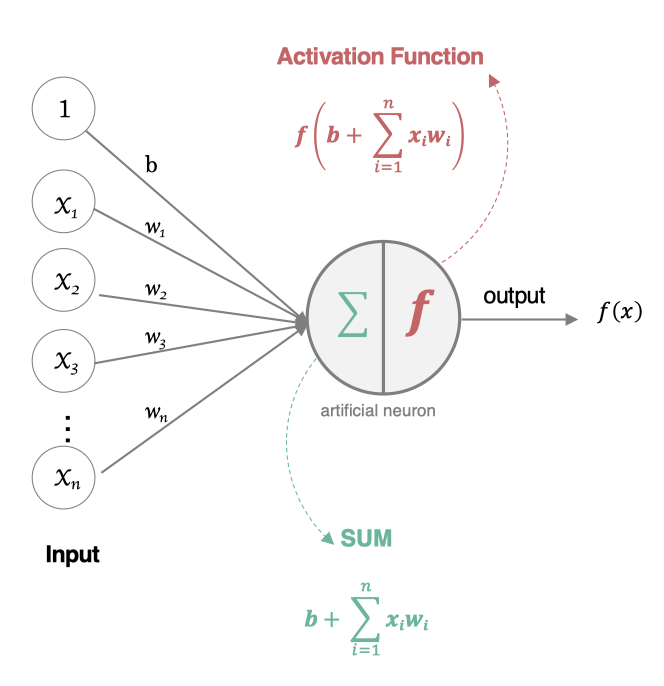
2、激活函数

在神经元中引入了激活函数，它的本质是向神经网络中引入“非线性” 因素，通过激活函数，神经网络就可以拟合各种曲线。如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，引入非线性函数作为激活函数，那输出不再是输入的线性组合，可以逼近任意函数。使得网络可以处理复杂的非线性数据关系。

常用的激活函数包括Sigmoid函数、Tanh函数和ReLU函数等。

a. Sigmoid函数

sigmoid 在定义域内处处可导，且两侧导数逐渐趋近于0。如果X的值很大或者很小的时候，那么函数的梯度（函数的斜率）会非常小，在反向传播的过程中，导致了向低层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。

一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象。而且，该激活函数并不是以 0 为中心的（是以 0.5 为中心的），所以在实践中这种激活函数使用的很少。sigmoid函数一般只用于二分类的输出层。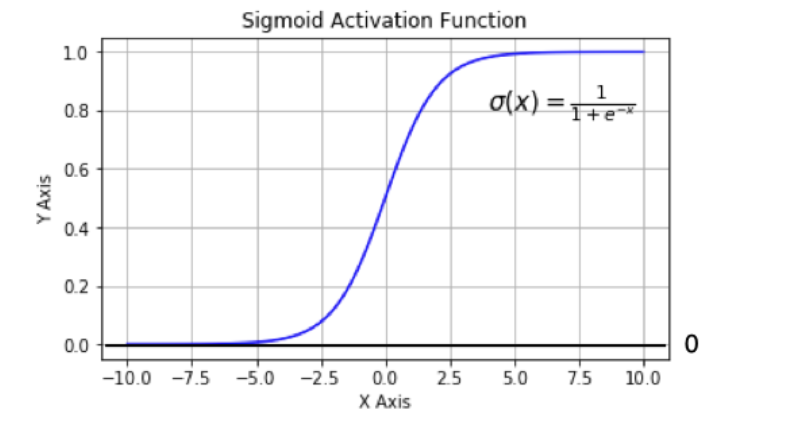

b. Tanh函数

tanh 也是一种非常常见的激活函数。与 sigmoid 相比，它是以 0 为中心的，使得其收敛速度要比 sigmoid 快（相比之下，tanh 曲线更为陡峭一些），减少迭代次数。然而，从图中可以看出，tanh 两侧的导数也为 0，同样会造成梯度消失。

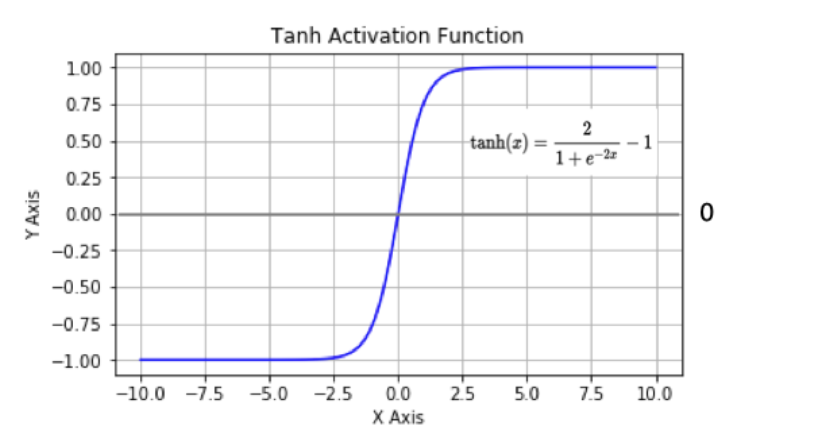
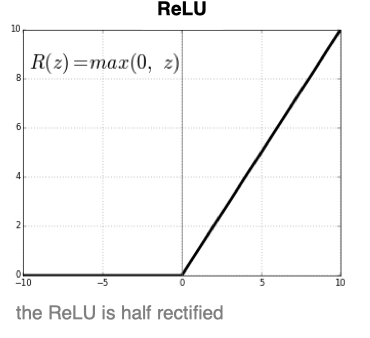
c. ReLU函数

ReLU是目前最常用的激活函数。数学表达式为：f(x) = max (0, x) 。从图中可以看到，当x<0时，ReLU导数为0，而当x>0时，则不存在饱和问题。所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。然而，随着训练的推进，部分输入会落入小于0区域，导致对应权重无法更新。这种现象被称为“神经元死亡”。

Relu是输入只能大于0, 如果你输入含有负数，Relu就不适合，如果你的输入是图片格式，Relu就挺常用的，因为图片的像素值作为输入时取值为[0,255]。

与sigmoid相比，RELU的优势是：

采用sigmoid函数，计算量大（指数运算），反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。
sigmoid函数反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。
Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。

3、网络基本组成

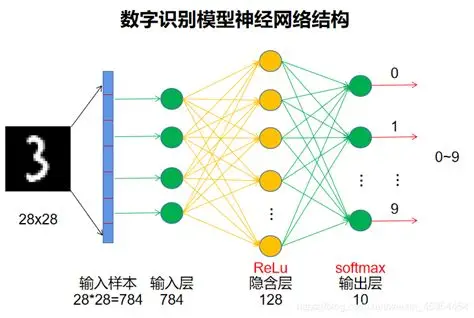
下面以使用MNIST数据集搭建一神经网络为例，介绍神经网络的基本组成部分和工作原理：

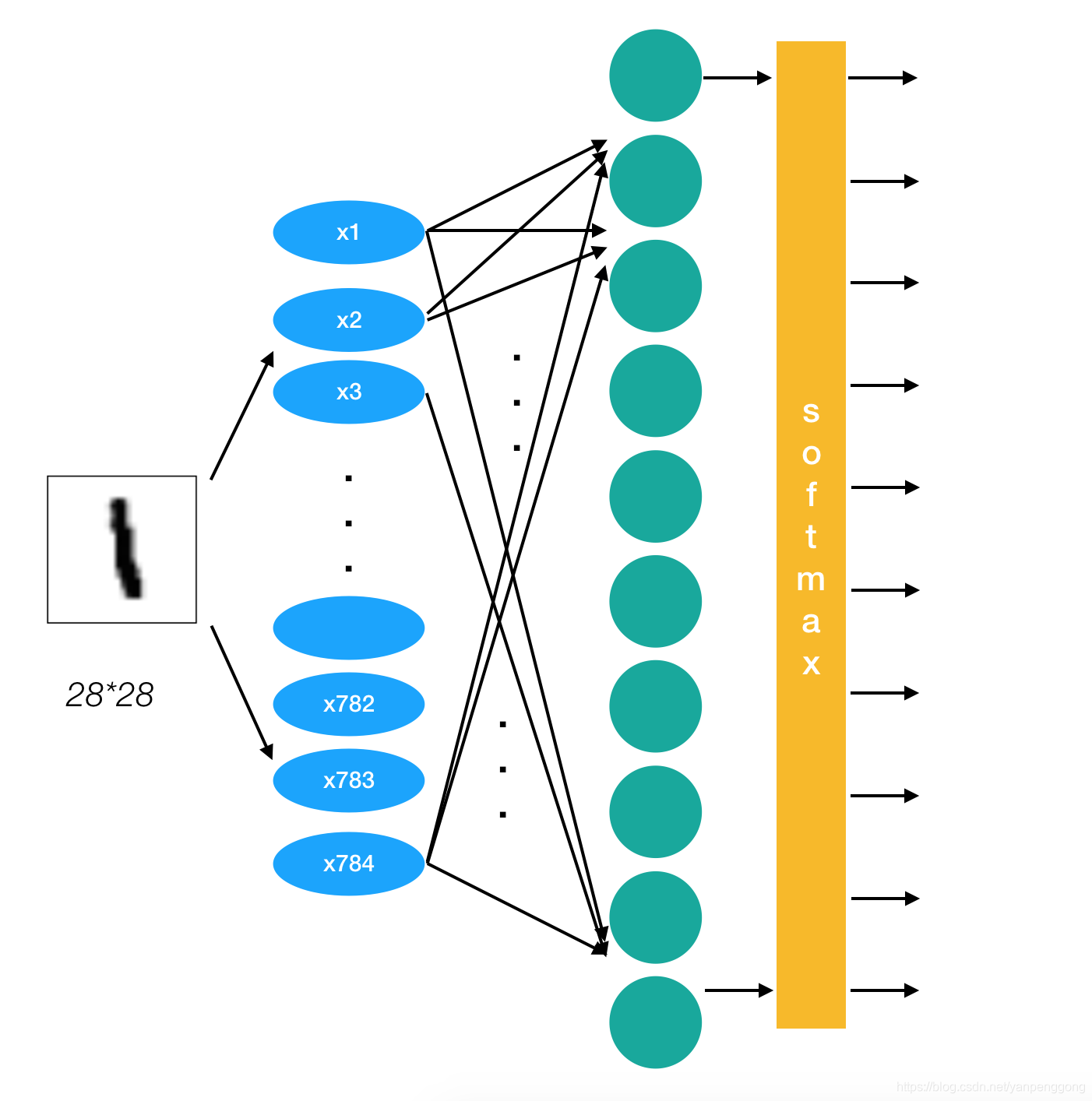
基本组成部分和MNIST网络样例

输入层：负责接收输入数据，每个节点（或神经元）对应一个输入特征。MNIST网络输入层有784个神经元对应于图像大小的28×28=784。
隐藏层：位于输入层和输出层之间，是神经网络的核心部分，负责提取和转换特征。MNIST神经网络配置k个隐藏层，第1个隐藏层有64个神经元，第2个隐藏层有64个神经元。这个隐藏层个数、神经元个数可以设置为任何值。
输出层：根据具体任务输出最终结果，神经元数量和激活函数的选择取决于任务类型。MNIST网络输出层的神经元数量为10，对应于数字0到9，共10类别的识别结果。
神经元：神经网络的基本计算单元，模拟了生物神经元的工作机制，通过加权求和和非线性激活函数处理后生成输出。

4、工作原理

神经网络的工作原理包括前向传播和反向传播两个过程。神经网络训练的过程就是调整权重参数值。

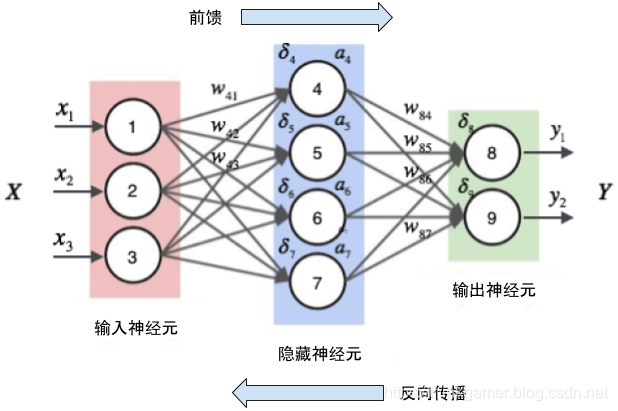
a. 前向传播（Forward Propagation）

前向传播是指将输入信号通过网络向前传递，经过一系列的加权求和和激活函数操作，最终得到输出结果的过程。

每一层的神经元计算加权和并应用激活函数。
最终输出层的预测值与真实值对比，计算损失（Loss）。

示例：MNIST手写数字识别中，输入层接收28×28像素图像，隐藏层提取边缘特征，输出层给出“数字是3”的概率。

b. 反向传播（Backpropagation）

反向传播工作目标是根据预测结果与真实值的误差，通过计算损失函数相对于每个权重的梯度，并沿着梯度的方向更新权重，以使损失函数最小化。

步骤：

计算梯度：通过链式法则（Chain Rule）从输出层向输入层逐层计算损失对每个参数的梯度。
参数更新：使用优化算法（如梯度下降）按梯度方向调整参数，使损失逐步降低。

神经网络反向传播算法（Backpropagation）通常归功于Rumelhart、Hinton和Williams的1986年《Nature》论文：”Learning representations by back-propagating errors” (Nature 323: 533-536)，使其成为现代深度学习的基础。解决多层网络训练难题：首次提供了高效计算梯度的方法，使得深度神经网络（尤其是全连接、CNN、RNN）的训练成为可能。该算法适用于大多数可微分的网络结构，为后续深度学习模型（如Transformer）奠定基础。2018年图灵奖授予Hinton/Bengio/LeCun时，IEEE特别指出反向传播是”使深度学习成为可能的基石性突破”。当前所有神经网络训练仍以该算法为基础，其PyTorch/TensorFlow实现已优化至单GPU每秒百万次反向传播计算。其经济价值包括：

直接推动2010年后AI产业爆发。
支撑计算机视觉/NLP等领域90%以上商业应用。
全球AI市场规模从2015年200亿增至2023年5000亿美元。

5、归一化

深度学习中归一化（Normalization）是一类用于调整神经网络中间层数据分布的技术，旨在解决训练过程中的梯度不稳定（如梯度消失/爆炸）、收敛速度慢或过拟合等问题。其核心思想是通过规范化输入或中间特征的数据分布。

常用的Softmax归一化（Softmax Normalization）是一种将实数向量转换为概率分布的函数，常用于多分类任务的输出层。它的核心思想是通过指数运算和归一化，将任意实数值的得分（logits-原始预测值、未归一化的得分）转化为概率，且所有输出概率之和为1。

6、应用领域

神经网络的应用领域非常广泛，包括图像识别、自然语言处理、推荐系统、金融预测、医疗诊断等。

神经网络通过模拟人脑的神经元网络结构，能够处理复杂的非线性问题，并在多个领域取得了显著的成果。随着技术的不断进步，神经网络的应用前景将更加广阔。

二、样例-MNIST手写数字识别

1. MNIST数据集

MNIST 数据集是计算机视觉领域中最重要的数据集之一，对于初学者和研究人员来说，它提供了一个相对简单但实用的平台来测试和训练机器学习模型。以下是关于MNIST数据集的一些关键信息：

数据集内容：MNIST 数据集包含手写数字的灰度图像，总共有10个类别（数字0到9）。
创建者：NIST
发布时间：1994年
图像大小：每张图像的尺寸是 28x28 像素。
数据集规模：训练集包含 60,000 张图像。测试集包含 10,000 张图像。
数据集特点：图像是标准化的，即它们被调整为固定大小，并且中心位于图像中心。图像是灰度的，即每个像素只有一个灰度值。
使用场景：由于其简单性和标准化，MNIST 数据集通常作为深度学习和机器学习入门教程的基准数据集。它被广泛用于训练和评估各种图像识别模型，包括卷积神经网络（CNN）。
深度学习框架支持：许多深度学习框架，如 TensorFlow、Keras、PyTorch 和 Caffe，都提供了内置的支持或易于使用的接口来加载和处理 MNIST 数据集。

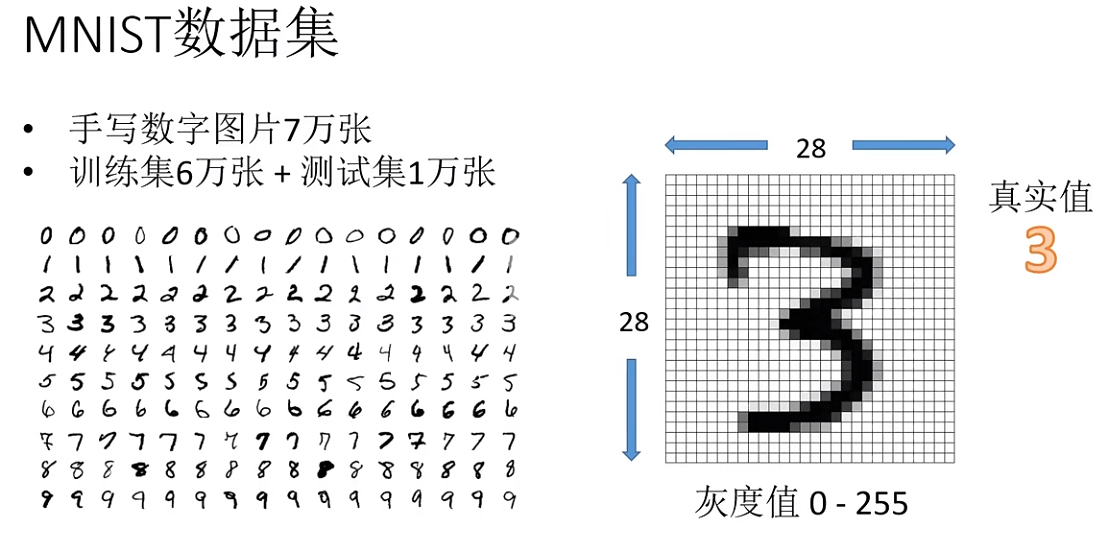
图：MNIST数据集内容

2. 数据集使用许可协议

MIT

三、样例实现

源码：pytorch-mnist.py

参考《安装深度学习框架PyTorch》，安装CPU版或GPU版PyTorch框架。以下为简化版安装方法：

conda create -n pytorch-env python=3.10
conda activate pytorch-env
conda install numpy pytorch torchvision matplotlib

1、加载开发包

import torch
from torch.utils.data import DataLoader
from torchvision import transforms
from torchvision.datasets import MNIST
import matplotlib.pyplot as plt

2、定义神经网络模型

以下代码这段代码使用PyTorch框架定义了一个简单的神经网络模型，该模型包含四个全连接层（也称为线性层），并使用 ReLU（Rectified Linear Unit）激活函数。ReLU函数定义为当输入大于或等于 0 时，函数值为输入本身；当输入小于 0 时，函数值为 0。

在 __init__ 方法中，我们定义了四个全连接层：

self.fc1：输入维度为 28 * 28（对应于 28×28 的图像），输出维度为 64。
self.fc2：输入维度为 64，输出维度为 64。
self.fc3：输入维度为 64，输出维度为 64。
self.fc4：输入维度为 64，输出维度为 10（对应于 10 类分类任务）。

forward 方法定义了数据在网络中的前向传播过程：

输入 x 首先通过 self.fc1 层，然后应用 ReLU 激活函数。
输出通过 self.fc2 层，再次应用 ReLU 激活函数。
输出通过 self.fc3 层，继续应用 ReLU 激活函数。
最后，输出通过 self.fc4 层，并应用 log_softmax 函数。log_softmax 函数将输出转换为对数概率分布，这在多分类任务中很常见。dim=1 参数表示沿着第二个维度（即类别维度）进行 softmax 操作。softmax()用于将一组任意实数转换为表示概率分布的[0,1]之间的实数。它本质上是一种归一化函数。

class Net(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = torch.nn.Linear(28*28, 64)
        self.fc2 = torch.nn.Linear(64, 64)
        self.fc3 = torch.nn.Linear(64, 64)
        self.fc4 = torch.nn.Linear(64, 10)
    
    def forward(self, x):
        x = torch.nn.functional.relu(self.fc1(x))
        x = torch.nn.functional.relu(self.fc2(x))
        x = torch.nn.functional.relu(self.fc3(x))
        x = torch.nn.functional.log_softmax(self.fc4(x), dim=1)
        return x

3、加载数据

def get_data_loader(is_train):
    to_tensor = transforms.Compose([transforms.ToTensor()])
    data_set = MNIST(root='.', train=is_train, transform=to_tensor, download=True)
    return DataLoader(data_set, batch_size=15, shuffle=True)

4、定义评估函数

这段代码定义了一个名为 evaluate 的函数，用于评估神经网络模型在测试数据集上的性能。

函数初始化两个计数器：

n_correct：用于记录模型预测正确的样本数量。
n_total：用于记录测试数据集中的总样本数量。

使用 with torch.no_grad() 上下文管理器可以确保在评估过程中不计算梯度，从而节省计算资源。

对于测试数据集中的每个样本（x, y），执行以下操作：

将输入特征 x 调整为模型所需的形状（在这里是 [batch_size, 28 * 28]，其中 batch_size 是批量大小）。
将调整后的输入特征传递给模型，并获取模型的输出 outputs。
对于每个输出 output，使用 torch.argmax 函数找到概率最高的类别索引，并将其与真实标签 y[i] 进行比较。如果它们相等，则将 n_correct 计数器加 1。
将 n_total 计数器加 1，表示已处理一个样本。

返回准确率：return n_correct / n_total 计算并返回模型在测试数据集上的准确率，即预测正确的样本数量除以总样本数量。

def evaluate(test_data, net):
    n_correct = 0
    n_total = 0
    with torch.no_grad():
        for (x, y) in test_data:
            outputs = net.forward(x.view(-1, 28*28))
            for i, output in enumerate(outputs):
                if torch.argmax(output) == y[i]:
                    n_correct += 1
                n_total += 1
    return n_correct / n_total

5、模型训练

定义了一个名为 main 的函数。定义一个 Adam 优化器，用于优化模型的参数。学习率设置为 0.001。

训练过程包含两个 epoch（迭代次数），每个 epoch 都遍历训练数据集。对于每个样本（x, y），执行以下操作：

使用 net.zero_grad() 清除之前的梯度。
将输入特征 x 调整为模型所需的形状（在这里是 [batch_size, 28 * 2GLU）。
将调整后的输入特征传递给模型，并获取模型的输出 output。
使用 torch.nn.functional.nll_loss 采用负对数似然损失函数计算损失。
使用 loss.backward() 计算梯度反向传播。PyTorch构建计算图（Computational Graph）跟踪所有张量操作。根据链式法则，从loss开始反向遍历计算图，计算每个参数的梯度。梯度值存储在参数的.grad属性中（如weight.grad）。
使用 optimizer.step() 更新模型的参数。

在每个 epoch 结束时，评估模型在测试数据集上的准确率，并打印出来。

可视化预测结果：遍历测试数据集的前四个样本，并对每个样本执行以下操作：

使用 torch.argmax 函数找到概率最高的类别索引。
使用 plt.imshow 函数显示输入图像。
使用 plt.title 函数显示预测结果。

最后，使用 plt.show() 显示所有图像。

def main():

    train_data = get_data_loader(is_train=True)
    test_data = get_data_loader(is_train=False)
    net = Net()
    
    print("initial accuracy:", evaluate(test_data, net))
    optimizer = torch.optim.Adam(net.parameters(), lr=0.001)
    for epoch in range(2):
        for (x, y) in train_data:
            net.zero_grad()
            output = net.forward(x.view(-1, 28*28))
            loss = torch.nn.functional.nll_loss(output, y)
            loss.backward()
            optimizer.step()
        print("epoch", epoch, "accuracy:", evaluate(test_data, net))

    for (n, (x, _)) in enumerate(test_data):
        if n > 3:
            break
        predict = torch.argmax(net.forward(x[0].view(-1, 28*28)))
        plt.figure(n)
        plt.imshow(x[0].view(28, 28))
        plt.title("prediction: " + str(int(predict)))
    plt.show()

if __name__ == "__main__":
    main()

6、推理运行结果

在data-code目录下执行：

python pytorch-mnist.py

Using downloaded and verified file: .\MNIST\raw\t10k-labels-idx1-ubyte.gz
Extracting .\MNIST\raw\t10k-labels-idx1-ubyte.gz to .\MNIST\raw

initial accuracy: 0.0982
epoch 0 accuracy: 0.9486
epoch 1 accuracy: 0.9669

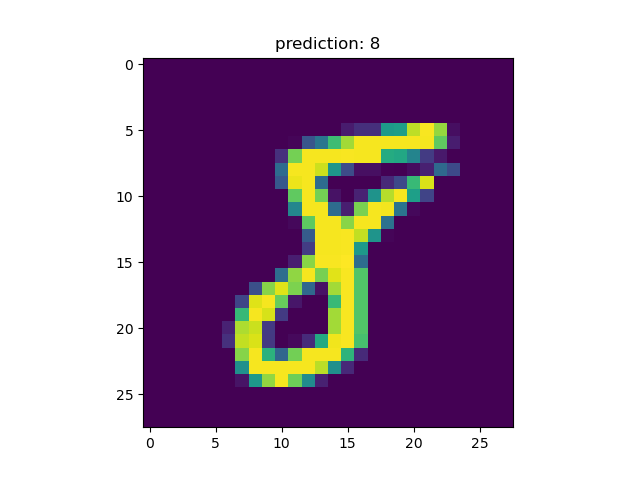
对于一手写字符为8的测试图片推理出分类8。

index in the last dimension changes the fastest.

五、获取案例套装